Introduction
The problem will use two data structures -- an ordered binary tree and a circular doubly linked list. Both data structures store sorted elements, but they look very different.
1. Ordered Binary Tree
In the ordered binary tree, each node contains a single data element and "small" and "large" pointers to sub-trees (sometimes the two pointers are just called "left" and "right"). Here's an ordered binary tree of the numbers 1 through 5...
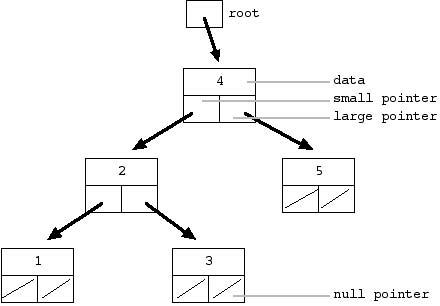
Figure-1 -- ordered binary tree
All the nodes in the "small" sub-tree are less than or equal to the data in the parent node. All the nodes in the "large" sub-tree are greater than the parent node. So in the example above, all the nodes in the "small" sub-tree off the 4 node are less than or equal to 4, and all the nodes in "large" sub-tree are greater than 4. That pattern applies for each node in the tree. A null pointer effectively marks the end of a branch in the tree. Formally, a null pointer represents a tree with zero elements. The pointer to the topmost node in a tree is called the "root".
2. Circular Doubly Linked List
Here's a circular doubly linked list of the numbers 1 through 5...
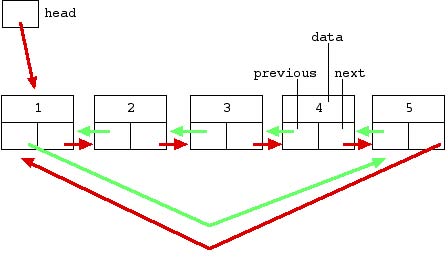
Figure-2 -- doubly linked circular list
The circular doubly linked list is a standard linked list with two additional features...
 "Doubly linked" means that each node has two pointers -- the usual "next" pointer that points to the next node in the list and a "previous" pointer to the previous node.
"Doubly linked" means that each node has two pointers -- the usual "next" pointer that points to the next node in the list and a "previous" pointer to the previous node.
 "Circular" means that the list does not terminate at the first and last nodes. Instead, the "next" from the last node wraps around to the first node. Likewise, the "previous" from the first node wraps around to the last node.
"Circular" means that the list does not terminate at the first and last nodes. Instead, the "next" from the last node wraps around to the first node. Likewise, the "previous" from the first node wraps around to the last node.
We'll use the convention that a null pointer represents a list with zero elements. It turns out that a length-1 list looks a little silly...
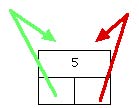
Figure-3 -- a length-1 circular doubly linked list
The single node in a length-1 list is both the first and last node, so its pointers point to itself. Fortunately, the length-1 case obeys the rules above so no special case is required.
The Trick -- Separated at Birth?
Here's the trick that underlies the Great Tree-List Problem: look at the nodes that make up the ordered binary tree. Now look at the nodes that make up the linked list. The nodes have the same type structure -- they each contain an element and two pointers. The only difference is that in the tree, the two pointers are labeled "small" and "large" while in the list they are labeled "previous" and "next". Ignoring the labeling, the two node types are the same.
3. The Challenge
The challenge is to take an ordered binary tree and rearrange the internal pointers to make a circular doubly linked list out of it. The "small" pointer should play the role of "previous" and the "large" pointer should play the role of "next". The list should be arranged so that the nodes are in increasing order...
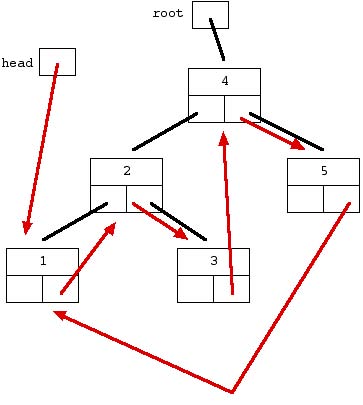
Figure-4 --original tree with list "next" arrows added
This drawing shows the original tree drawn with plain black lines with the "next" pointers for the desired list structure drawn as arrows. The "previous" pointers are not shown.
Complete Drawing
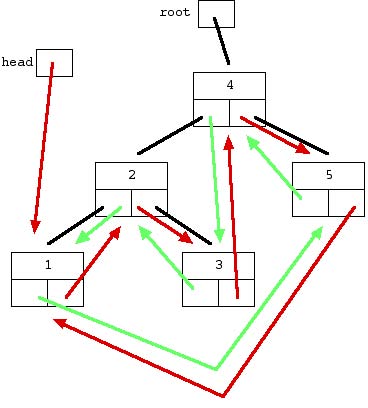
Figure-5 -- original tree with "next" and "previous" list arrows added This drawing shows the all of the problem state -- the original tree is drawn with plain black lines and the desired next/previous pointers are added in as arrows. Notice that starting with the head pointer, the structure of next/previous pointers defines a list of the numbers 1 through 5 with exactly the same structure as the list in figure-2. Although the nodes appear to have different spatial arrangement between the two drawings, that's just an artifact of the drawing. The structure defined by the the pointers is what matters.
4. Problem Statement
Here's the formal problem statement: Write a recursive function treeToList(Node root) that takes an ordered binary tree and rearranges the internal pointers to make a circular doubly linked list out of the tree nodes. The "previous" pointers should be stored in the "small" field and the "next" pointers should be stored in the "large" field. The list should be arranged so that the nodes are in increasing order. Return the head pointer to the new list. The operation can be done in O(n) time -- essentially operating on each node once. Basically take figure-1 as input and rearrange the pointers to make figure-2.
Try the problem directly, or see the hints below.
5. Lessons and Solution Code
The solution code is given below in Java and C. The most important method is treeToList() and the helper methods join() and append(). Here are the lessons I see in the two solutions...
-
Trust that the recursive calls return correct output when fed correct input -- make the leap of faith. Look at the partial results that the recursive calls give you, and construct the full result from them. If you try to step into the recursive calls to think how they are working, you'll go crazy.
-
Decomposing out well defined helper functions is a good idea. Writing the list-append code separately helps you concentrate on the recursion which is complex enough on its own.
Java Solution Code
// TreeList.java
/*
Demonstrates the greatest recursive pointer problem ever -
recursively changing an ordered binary tree into a circular
doubly linked list.
See http://cslibrary.stanford.edu/109/
This code is not especially OOP.
This code is free for any purpose.
Feb 22, 2000
Nick Parlante nick.parlante@cs.stanford.edu
*/
/*
This is the simple Node class from which the tree and list
are built. This does not have any methods -- it's just used
as dumb storage by TreeList.
The code below tries to be clear where it treats a Node pointer
as a tree vs. where it is treated as a list.
*/
class Node {
int data;
Node small;
Node large;
public Node(int data) {
this.data = data;
small = null;
large = null;
}
}
/*
TreeList main methods:
-join() -- utility to connect two list nodes
-append() -- utility to append two lists
-treeToList() -- the core recursive function
-treeInsert() -- used to build the tree
*/
class TreeList {
/*
helper function -- given two list nodes, join them
together so the second immediately follow the first.
Sets the .next of the first and the .previous of the second.
*/
public static void join(Node a, Node b) {
a.large = b;
b.small = a;
}
/*
helper function -- given two circular doubly linked
lists, append them and return the new list.
*/
public static Node append(Node a, Node b) {
// if either is null, return the other
if (a==null) return(b);
if (b==null) return(a);
// find the last node in each using the .previous pointer
Node aLast = a.small;
Node bLast = b.small;
// join the two together to make it connected and circular
join(aLast, b);
join(bLast, a);
return(a);
}
/*
--Recursion-
Given an ordered binary tree, recursively change it into
a circular doubly linked list which is returned.
*/
public static Node treeToList(Node root) {
// base case: empty tree -> empty list
if (root==null) return(null);
// Recursively do the subtrees (leap of faith!)
Node aList = treeToList(root.small);
Node bList = treeToList(root.large);
// Make the single root node into a list length-1
// in preparation for the appending
root.small = root;
root.large = root;
// At this point we have three lists, and it's
// just a matter of appending them together
// in the right order (aList, root, bList)
aList = append(aList, root);
aList = append(aList, bList);
return(aList);
}
/*
Given a non-empty tree, insert a new node in the proper
place. The tree must be non-empty because Java's lack
of reference variables makes that case and this
method messier than they should be.
*/
public static void treeInsert(Node root, int newData) {
if (newData<=root.data) {
if (root.small!=null) treeInsert(root.small, newData);
else root.small = new Node(newData);
}
else {
if (root.large!=null) treeInsert(root.large, newData);
else root.large = new Node(newData);
}
}
// Do an inorder traversal to print a tree
// Does not print the ending "\n"
public static void printTree(Node root) {
if (root==null) return;
printTree(root.small);
System.out.print(Integer.toString(root.data) + " ");
printTree(root.large);
}
// Do a traversal of the list and print it out
public static void printList(Node head) {
Node current = head;
while (current != null) {
System.out.print(Integer.toString(current.data) + " ");
current = current.large;
if (current == head) break;
}
System.out.println();
}
// Demonstrate tree->list with the list 1..5
public static void main(String[] args) {
// first build the tree shown in the problem document
// http://cslibrary.stanford.edu/109/
Node root = new Node(4);
treeInsert(root, 2);
http://cslibrary.stanford.edu/109/ TreeListRecursion.html
treeInsert(root, 1);
treeInsert(root, 3);
treeInsert(root, 5);
System.out.println("tree:");
printTree(root); // 1 2 3 4 5
System.out.println();
System.out.println("list:");
Node head = treeToList(root);
|
|
printList(head); |
// 1 2 3 4 5 |
yay! |
|
} |
|
|
|
|
} |
|
|
|
|
C Solution Code
/*
TreeList.c
C code version of the great Tree-List recursion problem.
See http://cslibrary.stanford.edu/109/ for the full
discussion and the Java solution.
This code is free for any purpose.
Feb 22, 2000
Nick Parlante nick.parlante@cs.stanford.edu
*/
#include <stdio.h>
#include <stddef.h>
#include <stdlib.h>
/* The node type from which both the tree and list are built */
struct node {
int data;
struct node* small;
struct node* large;
};
typedef struct node* Node;
/*
helper function -- given two list nodes, join them
together so the second immediately follow the first.
Sets the .next of the first and the .previous of the second.
*/
static void join(Node a, Node b) {
a->large = b;
b->small = a;
}
/*
helper function -- given two circular doubly linked
lists, append them and return the new list.
*/
static Node append(Node a, Node b) {
Node aLast, bLast;
if (a==NULL) return(b);
if (b==NULL) return(a);
aLast = a->small;
bLast = b->small;
join(aLast, b);
join(bLast, a);
return(a);
}
/*
--Recursion-
Given an ordered binary tree, recursively change it into
a circular doubly linked list which is returned.
*/
static Node treeToList(Node root) {
Node aList, bList;
if (root==NULL) return(NULL);
/* recursively solve subtrees -- leap of faith! */
aList = treeToList(root->small);
bList = treeToList(root->large);
/* Make a length-1 list ouf of the root */
root->small = root;
root->large = root;
/* Append everything together in sorted order */
aList = append(aList, root);
aList = append(aList, bList);
return(aList);
/* Create a new node */
static Node newNode(int data) {
Node node = (Node) malloc(sizeof(struct node));
node->data = data;
node->small = NULL;
node->large = NULL;
return(node);
}
/* Add a new node into a tree */
static void treeInsert(Node* rootRef, int data) {
Node root = *rootRef;
if (root == NULL) *rootRef = newNode(data);
else {
if (data <= root->data) treeInsert(&(root->small), data);
else treeInsert(&(root->large), data);
}
}
static void printList(Node head) {
Node current = head;
while(current != NULL) {
printf("%d ", current->data);
current = current->large;
if (current == head) break;
}
printf("\n");
}
/* Demo that the code works */
int main() {
Node root = NULL;
Node head;
treeInsert(&root, 4);
treeInsert(&root, 2);
treeInsert(&root, 1);
treeInsert(&root, 3);
treeInsert(&root, 5);
head = treeToList(root);
printList(head); /* prints: 1 2 3 4 5 */
return(0);
}
